Einführung in die pq Formel
Die pq Formel ist ein fundamentales Werkzeug in der Mathematik, insbesondere in der Algebra, zur Lösung quadratischer Gleichungen der Form x² + px + q = 0. Diese Formel wurde entwickelt, um effizient die Wurzeln solcher Gleichungen zu berechnen, die häufig in verschiedenen mathematischen und praktischen Anwendungen auftreten. Ihre Herkunft kann bis zu den Anfängen der Algebra zurückverfolgt werden, wobei Mathematiker über die Jahrhunderte Lösungen fanden, um quadratische Gleichungen zu bearbeiten.
Die pq Formel lautet: x = -p/2 ± √((p/2)² – q). Diese elegante Darstellung erleichtert nicht nur das Verständnis der Struktur quadratischer Gleichungen, sondern ermöglicht auch eine praktische Herangehensweise an die Berechnung ihrer Wurzeln. Durch ihre Anwendung können Mathematiker und Studierende schnell die Lösungen bestimmen, ohne auf komplexe Methoden zurückgreifen zu müssen.
In der Mathematik spielt die pq Formel eine entscheidende Rolle, nicht nur in der Theorie, sondern auch in der Praxis. Sie findet Anwendung in verschiedensten Bereichen wie Physik, Ingenieurwissenschaften sowie Wirtschaftswissenschaften, wo oft Modelle entwickelt werden, die auf quadratischen Gleichungen basieren. Zudem ist sie ein wesentlicher Bestandteil des Mathematikunterrichts, da sie den Schülern hilft, ein tieferes Verständnis für Funktionen und deren graphische Darstellungen zu entwickeln.
Abschließend lässt sich sagen, dass die pq Formel nicht nur eine technische Lösung darstellt, sondern auch ein Kernkonzept, das das mathematische Denken fördert. Ihre Anwendungen und Bedeutungen erstrecken sich über zahlreiche Disziplinen, was sie zu einem wichtigen Element der mathematischen Bildung und Praxis macht.
Die mathematischen Grundlagen der pq Formel
Die pq Formel ist ein bedeutsames Werkzeug in der Mathematik, insbesondere in der Algebra, um Lösungen der Form x² + px + q = 0 zu finden, wobei p und q Konstanten sind. Diese Gleichung beschreibt eine Parabel, und die pq Formel stellt einen effizienten Weg dar, um die Nullstellen dieser Parabel zu bestimmen. Zur Herleitung der pq Formel beginnen wir mit der klassischen quadratischen Gleichung und bringen diese in die sogenannte Normalform.
Die Umformung erfolgt durch komplettes Quadrat: Wir nehmen die rechte Seite der Gleichung und subtrahieren q und teilen p durch 2, was uns erlaubt, die Gleichung als (x + p/2)² = (p/2)² – q zu schreiben. Durch diesen Umformungsprozess gewinnen wir die Grundform, die es uns ermöglicht, die Lösungswerte für x zu isolieren.
Die Variablen in dieser Gleichung haben folgendes zu bedeuten: x ist die gesuchte Unbekannte, p repräsentiert die Koeffizienten, die an x gebunden sind, und q stellt den konstanten Term dar. Mit dieser Herleitung können wir die Nullstellen mit Hilfe der Gleichung x = -p/2 ± √((p/2)² – q) berechnen.
Um diese Konzepte weiter zu veranschaulichen, nehmen wir an, dass p = 4 und q = 3. Setzen wir diese Werte in die pq Formel ein, erhalten wir die Lösungen: x = -4/2 ± √((4/2)² – 3), was sich zu x = -2 ± √(4 – 3) vereinfacht, und letztlich die Nullstellen x = -1 und x = -3 ergeben kann. Diese Resultate zeigen deutlich, wie die pq Formel sowohl theoretisch als auch praktisch in der Mathematik Anwendung findet.
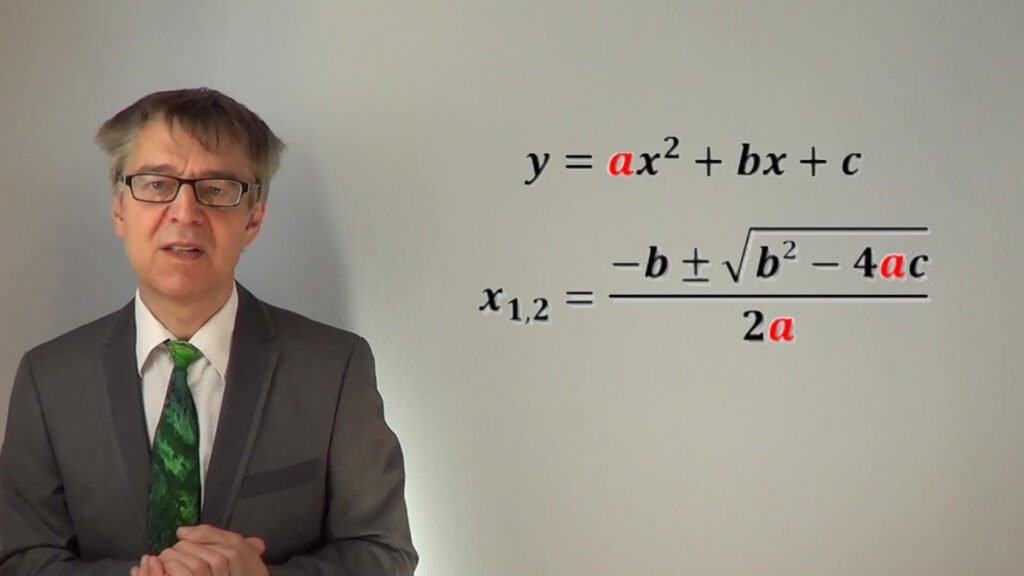
Praktische Anwendungen der pq Formel
Die pq Formel ist ein entscheidendes Werkzeug, das in zahlreichen Disziplinen erhebliche Anwendung findet. Insbesondere in der Mathematik und Naturwissenschaften ist sie ein bewährtes Mittel zur Lösung von Gleichungen quadratischer Form. Sie ist von zentraler Bedeutung, um Wurzeln aus solchen Gleichungen zu ziehen, was in praktischen Szenarien oft notwendig ist.
In der Physik wird die pq Formel häufig zur Berechnung von Bewegungen eingesetzt. Zum Beispiel bei der Analyse von Wurfbewegungen kann sie verwendet werden, um die Zeitpunkte zu ermitteln, an denen ein Objekt eine bestimmte Höhe erreicht. In solchen Fällen wird die Gleichung der Bewegung in die Form einer quadratischen Gleichung umformuliert, sodass die Lösung durch die Anwendung der pq Formel erfolgt. Dadurch lässt sich präzise vorhersagen, wann und wo ein Objekt landet, was für Ingenieure und Physiker von essentieller Bedeutung ist.
Die Technik nutzt die pq Formel ebenso in der Elektrotechnik, beispielsweise zur Berechnung von elektrischen Schaltungen. Hier können Gleichungen zur Bestimmung der Spannungsabfälle oder der Stromstärke aufgestellt werden, die in Quadro-Form gebracht sind. Die Fähigkeit, diese Gleichungen mithilfe der pq Formel zu lösen, ermöglicht es Ingenieuren, effizientere und sicherere Designs zu entwickeln.
Im wirtschaftlichen Bereich wird die pq Formel verwendet, um Investitionsentscheidungen zu bewerten und Kostenanalysen durchzuführen. Durch die Modellierung von Gewinn und Verlust über die Zeit können Unternehmer die optimale Strategie zur Umsatzmaximierung oder Kostenminimierung bestimmen. Die Anwendung der pq Formel bietet eine quantitative Grundlage, um fundierte Entscheidungen zu treffen und Risiken besser zu bewerten.
Fazit und weiterführende Ressourcen zur pq Formel
Die pq Formel spielt eine zentrale Rolle in der algebraischen Mathematik, vor allem bei der Lösung von quadratischen Gleichungen. Sie bietet eine systematische Methode, um Lösungen für Gleichungen in der Form x² + px + q = 0 zu finden. In diesem Rahmen hat die pq Formel nicht nur theoretische, sondern auch praktische Relevanz, da sie in verschiedenen Anwendungsgebieten, von der Naturwissenschaft bis zur Technik, eingesetzt wird. Das Verständnis und die Anwendung dieser Formel ist daher für Studierende und Fachleute gleichermaßen von Bedeutung.
Es ist wichtig, die erlernten Konzepte aktiv in der Praxis zu nutzen. Das Anwenden der pq Formel auf unterschiedliche Probleme fördert nicht nur das mathematische Verständnis, sondern stärkt auch die Fähigkeit, analytisch zu denken. Studierende sind ermutigt, Aufgaben und Übungen durchzuführen, um ihre Kenntnisse zu vertiefen und die Mechanismen hinter der pq Formel zu meistern.
Für diejenigen, die ihr Wissen erweitern möchten, gibt es eine Vielzahl von Ressourcen. Bücher über Algebra und Übungshefte zu quadratischen Gleichungen bieten ausgezeichnete Möglichkeiten zur Vertiefung des Themas. Weiterhin gibt es viele Online-Kurse und Tutorials, die speziell auf die pq Formel und verwandte Themen eingehen. Plattformen wie Khan Academy oder Coursera stellen oft kostenfreie sowie kostenpflichtige Inhalte zur Verfügung, die eine strukturierte und interaktive Lernerfahrung gewährleisten. Der Austausch in Foren und Communitys kann ebenfalls förderlich sein, um Fragen zu klären und verschiedene Lösungsansätze zu diskutieren.
Zusammenfassend lässt sich sagen, dass die Beherrschung der pq Formel, unterstützt durch entsprechende Ressourcen, jedem helfen kann, seine mathematischen Fähigkeiten erheblich zu verbessern.

